Quantum Entanglement to cheat the Reality

Quantum entanglement

Have you ever thought of a situation when the happening of an event in an isolated environment dictates the result of another event also in an isolated environment with no communication allowed? That sounds infeasible in our view of reality, except that these two separated events share a somewhat telepathic power. Yes, this telepathy really happens in the realm of quantum entanglement. The phenomenon can be simplified that the result of the first measurement reveals information about the result of the second measurement despite an absolute separation and no communication setting.

In a two-qubit system, the general state can be reduced into $\displaystyle{\left|\Psi\right\rangle = \frac{1}{\sqrt{2}} \left(\left|00\right\rangle + \left|11\right\rangle \right)}$. Because this state cannot be factored into seperate individual states, the two qubits are entangled. Trong and his crush are playing a game: Each hold one qubit of the entangled pair and move far away from the other.

Assume Trong keeps the first qubit, while his crush takes care of the second one. If Trong conducts a measurement on his qubit, he will get $\left|0\right\rangle$ or $\left|1\right\rangle$ with equal probability of 50%. The situation will be the same if his crush measures the second qubit independently.

What draws our interest is the fact that when Trong finishes his measurement, the combined state of the system collapses in accordance to whatever the result he got: $\left|\Psi\right\rangle = \left|00\right\rangle$ if Trong got $\left|0\right\rangle$, or $\left|\Psi\right\rangle = \left|11\right\rangle$ if Trong got $\left|1\right\rangle$. The result of his measurement on the first qubit indirectly informs Trong on the result of the second measurement if it is conducted. This phenomenon always happens instantly regardless of space, which means Trong can foresee the result of a action supposed to be probabilistic, i.e. the second measurement, even though his crush can be light-years away from him.

This experiment was first named EPR paradox after physicists Albert Einstein, Boris Podolsky, and Nathan Rosen. The result seems unreasonable as it seems that it allows information to be transmitted faster than light (“spooky action at a distance” - Einstein), which is forbidden by the Theory of Relativity. The three physicists rejected the result by asserting that there are undetected hidden variables inside of the system responsible for the phenomenon, and stating the principle of locality that physical processes take place at one place should have no immediate effect on the reality at another location. Therefore, they call quantum mechanics an incomplete theory. However, their hidden variable theories were proven wrong by John Bell in 1964, followed by numerous experimental results that statistically confirm the likeliness of the correlation of the phenomenon and quantum mechanics.

Quantum entanglement nevertheless doesn’t hack the reality by outrunning the speed of light, and has nothing no compare with Thanos’s Reality Stone. In fact, this quantum phenomenon doesn’t really allow communicating faster than light, i.e. not violate the Theory of Relativity. Although Trong can infer the result of the second measurement by the time of the first measurement, he needs to transmit this piece of information to his crush via classical means, which are absolutely slower than the speed of light. Otherwise, his crush has no idea which result will come out. In this case, the second measurement appears perfectly probabilistic to his crush although it was secrectly determined after the first measurement. The obscure interaction between the two entangled qubits is called coordination instead of communication in order to avoid the lightspeed conflict.

CSHS game

Today Trong and his crush want to play another game with the following rule. Each one takes an input selected from ${0,1}$ in fair random. With that number, they each have to output a binary number, $0$ or $1$. To win the game, two outputs must be different if both inputs are $1$, or two outputs must be the same in all other three cases.

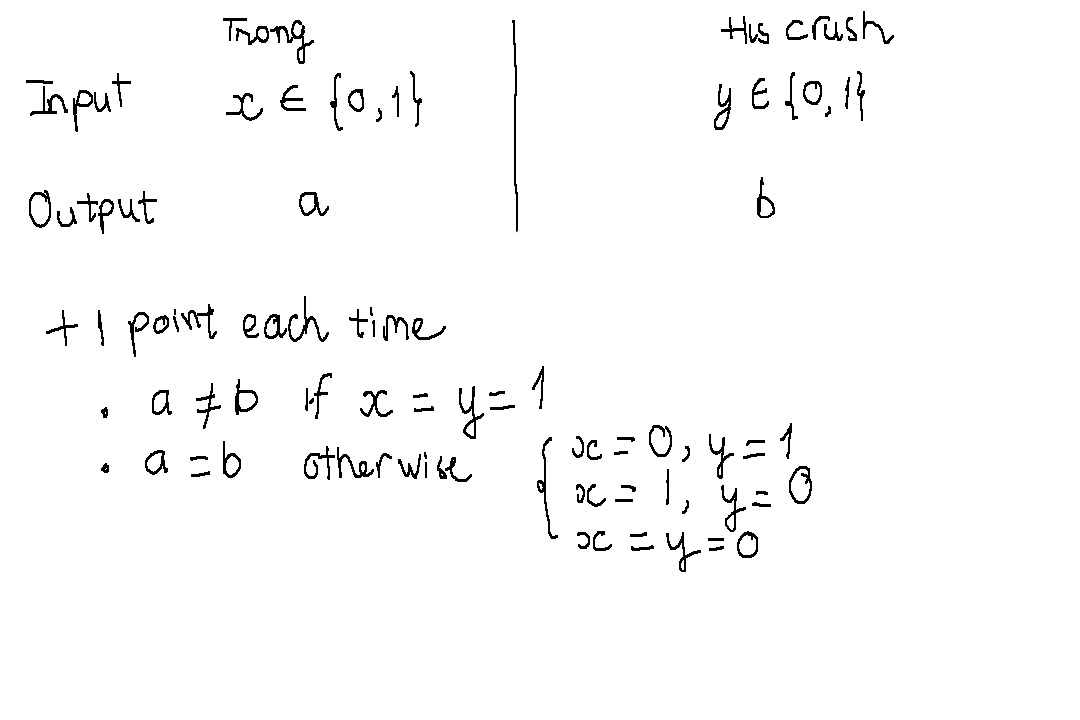
The win condition can be summerized as $$xy = (a + b)\mod 2 = a \oplus b$$ Because the inputs are uniformly random, Trong and his crush decide to always output $a=b$ to win in three out of four possible situations. 75% is also the highest success rate they can achieve in any kind of classical scenario. However, if they have the knowledge about quantum entanglement, they can raise their success rate up to $\cos^2{\frac{\pi}{8}}\approx 0.85$.

First, the two players need to share a pair of two qubits entangled in a Bell state and will take their measurements for the outputs. $$\left|\Psi\right\rangle = \frac{1}{\sqrt{2}}\left|00\right\rangle + \frac{1}{\sqrt{2}}\left|11\right\rangle$$ Depending upon the input value, they will measure their qubit in the corresponding basis.

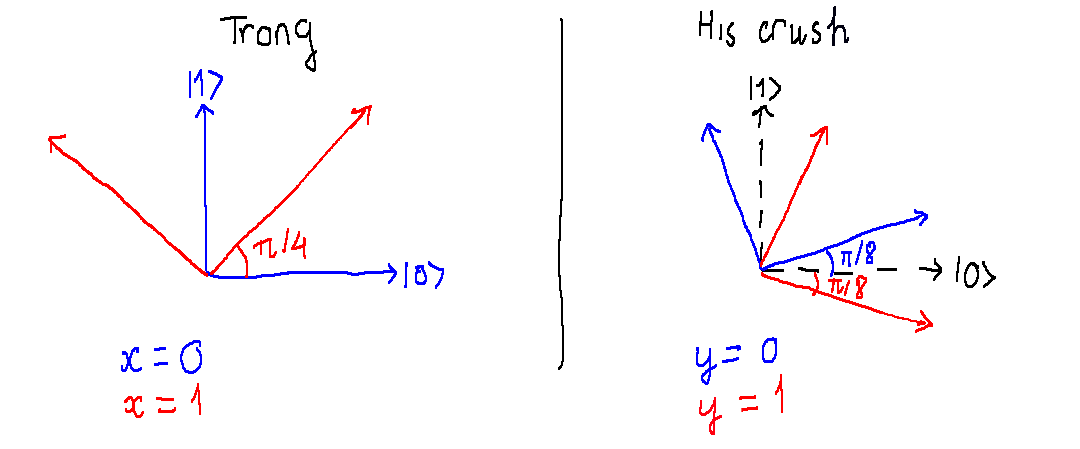
Due to the entanglement, when Trong gets $\left|0\right\rangle$ in his measurement, the state of the second qubit immediately becomes $\left|0\right\rangle$ while a $\left|1\right\rangle$ is followed by another $\left|1\right\rangle$. Following the intruction for measuring above, they can succeed with probability $\cos^2{\frac{\pi}{8}} > 0.75$ regardless of the input values.

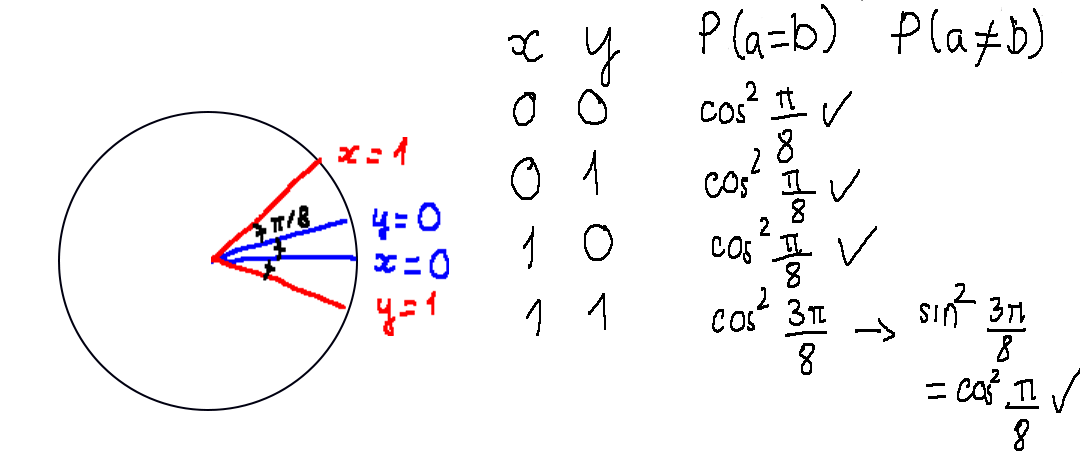
Here’s my code for calculating the success rate of this game in quantum scenario. It’s noticeable that quantum states of a single qubit are represented by complex numbers in 3-dimensional space. We however still can accomplish this following the same way we discussed above since we can transform the current state from the standard basis into the chosen basis through a rotation about the $y$-axis $$R_y(\theta):=e^{-i\theta\sigma_y/2} = \begin{bmatrix}\cos{\frac{\theta}{2}} & -\sin{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}}\end{bmatrix}$$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

 // Function measuring qubit states in a specific basis
 // Measure in a basis = Rotate to that basis + Measure in standard basis
 operation Rotate_Measure (alpha: Double, q: Qubit): Int {
	// Revolve aroung the Pauli Y axis
	Ry(2.0 * alpha, q);
	let m = M(q);
	Ry(-2.0 * alpha, q);
	if (m == One) {
		return 1;
	}
	return 0;
 }
    
 operation CHSH_Game (count: Int) : Int {
	mutable win = 0;
	mutable x = 0;
	mutable y = 0;
	mutable a = 0;
	mutable b = 0;

	using (qs = Qubit[2]) {
		for (test in 0 .. count) {
			set x = RandomInt(2);
			set y = RandomInt(2);
			set a = 0;
			set b = 0;

			H(qs[0]);
			CNOT(qs[0],qs[1]);

			if (x == 0) {
				if (M(qs[0]) == One) {
					set a = 1;
				}
			}	
			else {
				set a = Rotate_Measure(PI()/4.0, qs[0]);
			}

			if (y == 0) {
				set b = Rotate_Measure(PI()/8.0, qs[1]);
			}
			else {	
				set b = Rotate_Measure(-PI()/8.0, qs[1]);
			}

			if (x*y == (a+b) % 2) {
				set win = win + 1;
			}
			ResetAll(qs);
		}
	}
	return win;
 }
 

I repeated the game for 1000 times and counted the number of success that was in line with our prediction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

    class Driver {
        static void Main(string[] args)
        {
            using (var qsim = new QuantumSimulator())
            {
                var res = CHSH_Game.Run(qsim, 1000).Result;
                System.Console.WriteLine(
                  $"Your win rate is {res}/1000");
                Console.WriteLine("Press any key to continue...");
                Console.ReadKey();
            }
        }
    }
 

Click here to see a quantum-based proof of the optimal strategy for the CHSH game. By the way, the source code for this game is here. Check it out.