Quantum Teleportation (Part 2): The Art of transporting the Unknown

Problem Statement

Suppose Trong has just created a wonderful qubit in his lab. He knows his qubit look like $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$ but doesn’t know $\alpha$ and $\beta$. Now he wants to transport this qubit to his crush, but they don’t have a quantum channel that can help transport quantum information. Of course it’s a very bad idea for Trong to try to figure out $\alpha$ and $\beta$ through measurement because if he does so, he’ll destroy his qubit but only learn extremely little information about it. So how can Trong possibly transport his qubit to his crush. The key here is Quantum Teleportation.

No, teleportation doesn’t violate the No-cloning Theorem discussed in Part 1. Teleportation doesn’t mean duplicating a qubit or knowning its state, but just bringing it to another location.

For ease of writing, I’ll use letter A to indicate Trong and B for his crush in the next sections.

A Simplifed Solution

This is a completely unrealistic solution where we’re going to assume that there is a CNOT gate extending from A to B despite the large distance. We just examine this as a stepping stone for a realistic process later.

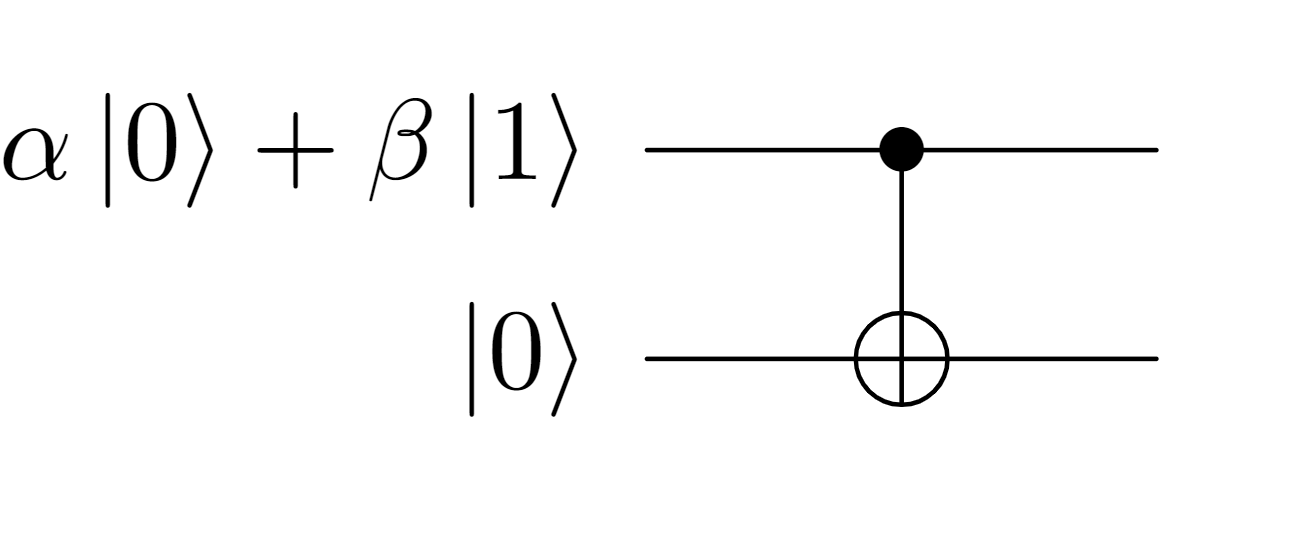
As shown in the figure above, A holds the top qubit in the state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$, and B keeps the bottom qubit $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$. The CNOT gate takes A’s qubit as the control and B’s as the target and entangles them into $|\psi\rangle = \alpha |00\rangle + \beta |11\rangle$.

Now one thing you may think of is to let A measure his qubit. If A gets a $|0\rangle$ then B also gets $|0\rangle$, and if A sees a $|1\rangle$ then B ends up with a $|1\rangle$. This is no good at all.

But what if A measures his qubit in the $|+\rangle,|-\rangle$ basis: $$\begin{matrix} \alpha |00\rangle + \beta |11\rangle &=& \displaystyle{\alpha \left(\frac{1}{\sqrt{2}}|+\rangle +\frac{1}{\sqrt{2}}|-\rangle \right) |0\rangle + \beta\left(\frac{1}{\sqrt{2}}|+\rangle -\frac{1}{\sqrt{2}}|-\rangle \right) |1\rangle } \\ &=& \displaystyle{\frac{1}{\sqrt{2}} |+\rangle \left(\alpha |0\rangle + \beta|1\rangle \right) + \frac{1}{\sqrt{2}}|-\rangle \left(\alpha |0\rangle - \beta|1\rangle \right)} \end{matrix}$$

If A gets $|+\rangle$, the composite state becomes $|+\rangle \left(\alpha |0\rangle + \beta|1\rangle \right)$.

On the contrary, if A gets $|-\rangle$, the composite state will be $|-\rangle \left(\alpha |0\rangle - \beta|1\rangle \right)$.

After his measurement, A just simply call and tell B the outcome, and B will need to use operator $Z =\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$ in case of receiving the outcome $|-\rangle$ from A. $Z$ operator do nothing to $|0\rangle$ state but flip the sign of $|1\rangle$ state.

In conclusion, if B receives the outcome $|+\rangle$, B already got the state $\alpha |0\rangle + \beta |1\rangle$ at hand. Otherwise, B applies a $Z$ and comes up with $Z \left( \alpha |0\rangle - \beta |1\rangle \right) = \alpha |0\rangle + \beta |1\rangle$ as we need. That’s how an over-stretching CNOT gate helps transmit a qubit from A to B, but I know that kind of gate still doesn’t exist in the world. In fact, this simplified solution points out we just need to create the entangled state $\psi\rangle = \alpha |00\rangle + \beta |11\rangle$ to do teleportation. We’ll make it without a quantum communication, i.e. the lengthy CNOT gate, in the next section.

Teleporting Procedure

Let’s assume A and B share a pair of qubits entangled in the state $|\psi\rangle = \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|11\rangle$. Generally speaking, teleportation is a protocol in which A measures two qubits, the entangled qubit and the unknown qubit that A wants to transport to B. Then, A makes a phone call and tells B two classical bits resulting from the measurements. Finally, B needs to apply some simple operators depending on the classical bits to restore the state of the unknown qubit. The following digram summarizes the crucial steps for a teleportation.

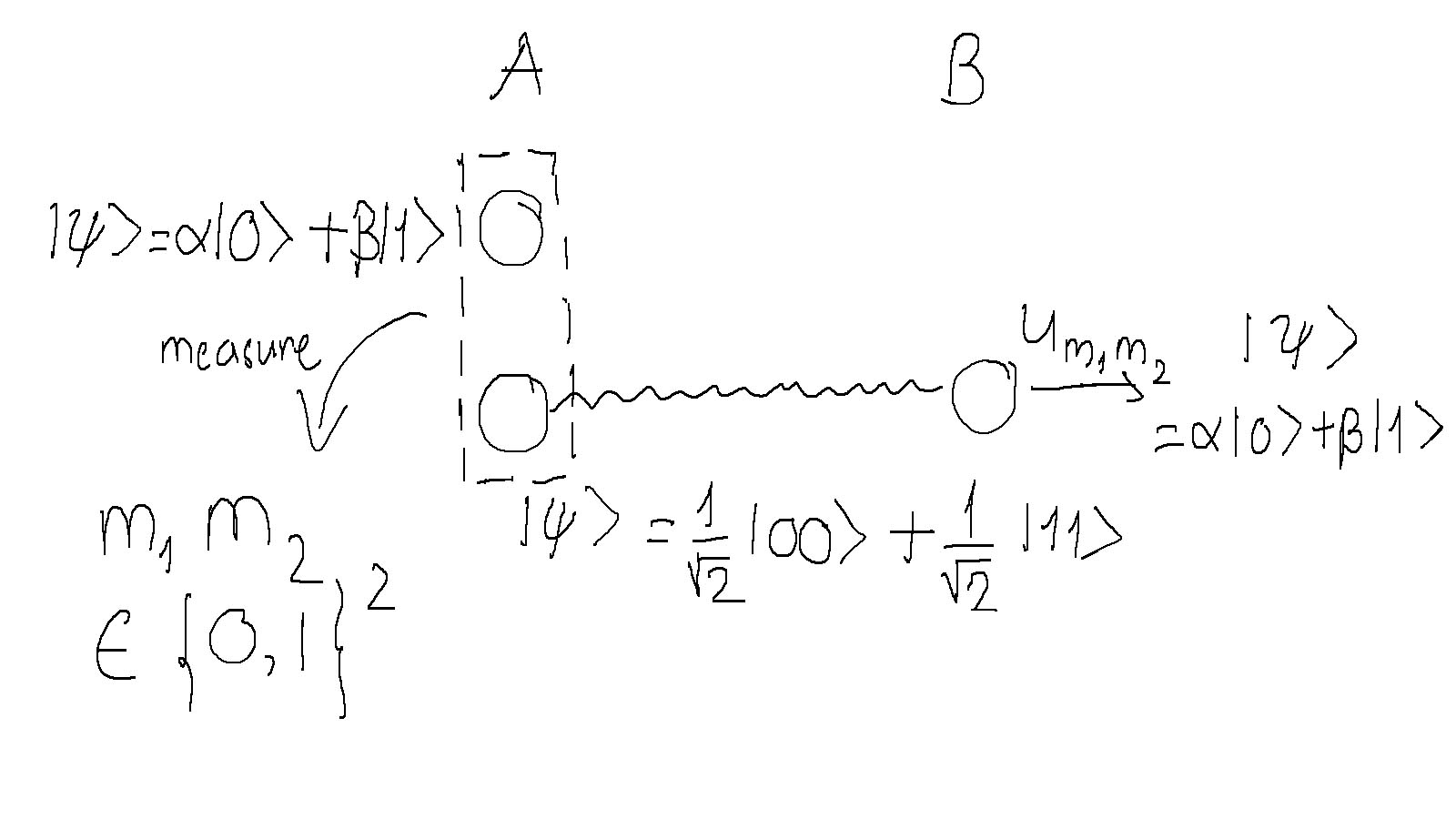
From then on, you shall know that all steps needed to perform a quantum algorithm can be shown in quantum circuit diagram as every classical algorithm has its own block diagram. Below is the complete quantum circuit for teleportation. Some new notations include big black dots as target nodes, dash-line rectangles as groupings that serve for clear visual as well as logical thinking flow, and double lines as classical wires (in contrast to single lines demonstrating quantum connections).

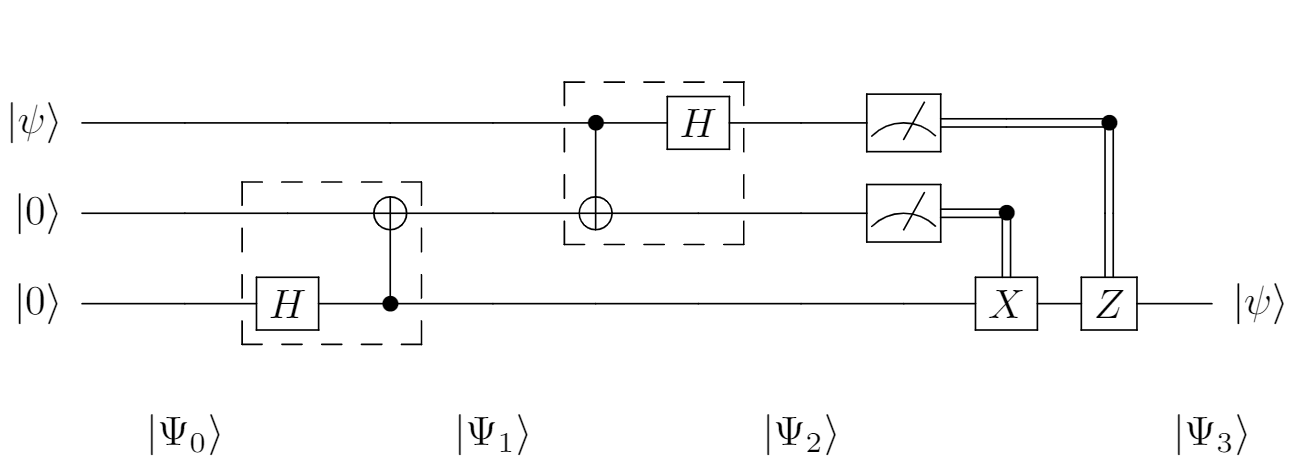
As you can see, there are three qubits in total, the top two of which will be measured on the A side later, and the bottom one on the B side will end up being in the $|\psi\rangle$ that A wants to transport. The second and third qubits need to be entangled before separated and each brought to one of the two people. The first grouping is responsible for that entanglement, which I call the preparation stage.

Preparation stage

$$|\Psi_0\rangle = (\alpha|0\rangle + \beta|1\rangle) |00\rangle$$ The first grouping alone is a Bell State circuit shown in Part 1 of this topic that if $|00\rangle$ is feeded as the input, the output state will be $|\Phi^+\rangle$. So that the beginning state $|\Psi_0\rangle$ evolves to $$\begin{matrix} |\Psi_1\rangle &=& \displaystyle{(\alpha|0\rangle + \beta|1\rangle) \left( \frac{1}{\sqrt{2}} |00\rangle + \frac{1}{\sqrt{2}} |11\rangle \right)} \\ &=& \displaystyle{\frac{\alpha}{\sqrt{2}} |000\rangle + \frac{\alpha}{\sqrt{2}} |011\rangle + \frac{\beta}{\sqrt{2}} |100\rangle + \frac{\beta}{\sqrt{2}} |111\rangle}\end{matrix}$$ Then the middle qubit will be delivered to A and the bottom one to B. They now share a pair of entangled qubits that will soon be helpful in forming a connection the unknown qubit with the B side.

Pre-measurement stage

This stage is wrapped into two operators inside the second grouping, a CNOT gate that takes the top qubit as the control and the middle as the target followed by a Hadamard gate acting on the first line.

You may be tempting to ask what are the purposes of these two gates. Do you remember the simplified solution we discussed above: A and B take advantage of entangling the unknown qubit at the source with the qubit at the destination. The CNOT gate here do the same thing in a slightly different manner. It entangles the top qubit to the second and therefore creates a cluster of three entangled qubits. $$|\Psi_{1.5}\rangle = \frac{\alpha}{\sqrt{2}} |000\rangle + \frac{\alpha}{\sqrt{2}} |011\rangle + \frac{\beta}{\sqrt{2}} |110\rangle + \frac{\beta}{\sqrt{2}} |101\rangle$$

Let me remind you that a qubit measurement in the $|+\rangle, |-\rangle$ basis, the most essential step in the simplified solution, is completely equivalent to rotating that qubit to the Hadamard basis (another name for $|+\rangle, |-\rangle$ basis) and then measuring it in the computational basis. This technique of rotating and measuring is frequently used as a subroutine in many quantum algorithms. Knowing the technique, A knows he needs to rotate the unknown qubit to the Hadamard basis using the Hadamard gate.

$$\begin{matrix} |\Psi_{2}\rangle &=& \displaystyle{\frac{\alpha}{\sqrt{2}} \left( \frac{1}{\sqrt{2}} |0\rangle + \frac{1}{\sqrt{2}} |1\rangle \right) (|00\rangle + |11\rangle) + \frac{\beta}{\sqrt{2}} \left( \frac{1}{\sqrt{2}} |0\rangle - \frac{1}{\sqrt{2}} |1\rangle \right) (|10\rangle + |01\rangle)} \\ &=& \displaystyle{\frac{\alpha}{2} (|000\rangle +|011\rangle + |100\rangle + |111\rangle) + \frac{\beta}{2} (|010\rangle +|001\rangle - |110\rangle - |101\rangle)} \\ &=& \displaystyle{\frac{1}{2} |00\rangle (\alpha |0\rangle + \beta|1\rangle) + \frac{1}{2} |01\rangle (\alpha |1\rangle + \beta|0\rangle) + \frac{1}{2} |10\rangle (\alpha |0\rangle - \beta|1\rangle) + \frac{1}{2} |11\rangle (\alpha |1\rangle - \beta|0\rangle)} \end{matrix}$$

Measurement stage

This last stage include two measurements and two controlled gates acting on the bottom qubit: Z controlled by the first qubit measurement and X by the second qubit measurement. The last equality shown in the pre-measurement stage has already revealed four possible situations of the two measurements A would perform. Let $b_0$ and $b_1$ be the upcoming results of the measurements for the top qubit and the middle qubit respectively. Which stages the bottom qubit is left in each case is shown in the table below.

$b_0b_1$	Bottom qubit
$00$	$\alpha |0\rangle + \beta|1\rangle$
$01$	$\alpha |1\rangle + \beta|0\rangle$
$10$	$\alpha |0\rangle - \beta|1\rangle$
$11$	$\alpha |1\rangle - \beta|0\rangle$

After the measurements, A picks up his phone and tells B the two outcomes to help B apply suitable operators to the third qubit. B will need to use $Z$ gate if $b_0 = 1$ and use $X$ gate if $b_1 = 1$. The order in which B applies operators doesn’t matter; you can verify that $XZ|\psi\rangle = ZX|\psi\rangle$ by doing some matrix calculations on your own. However, I want to let you know that when scientists write $U_1 U_0|\psi\rangle$, they mean to apply $U_0$ before $U_1$, i.e. operators will act on the qubit in the right-left order. Get back to the current problem, all the former states, after corresponding operations, have to transform into the unknown state.

$b_0b_1$	Bottom qubit
$00$	$\alpha |0\rangle + \beta|1\rangle \overset{I}{\rightarrow}\alpha|0\rangle + \beta|1\rangle$
$01$	$\alpha |1\rangle + \beta|0\rangle \overset{X}{\rightarrow}\alpha|0\rangle + \beta|1\rangle$
$10$	$\alpha |0\rangle - \beta|1\rangle \overset{Z}{\rightarrow}\alpha|0\rangle + \beta|1\rangle$
$11$	$\alpha |1\rangle - \beta|0\rangle \overset{ZX}{\rightarrow}-\alpha|0\rangle - \beta|1\rangle$

Now the qubit on B side is guaranteed to be in the state $\alpha |0\rangle + \beta|1\rangle$ except for the $b_0 b_1 = 11$ case. But don’t worry, two minus signs in $-\alpha|0\rangle - \beta|1\rangle$ are rather a global phase and experimentally undetectable. So that in all cases, Trong has successfully transported his qubit to his crush by communicating only two classical bits $b_0$ and $b_1$.

Recap

The whole algorithm for teleportation protocol can be described in a single line of states and operators that $$ (\mathbf{C^Z_{20} C^X_{21}})(\mathbf{M_1M_0})(\mathbf{H_0 CNOT_{10}})(\mathbf{CNOT_{12} H_2})(\alpha |0\rangle + \beta|1\rangle) |0\rangle |0\rangle$$ where $\mathbf{C^U_{ij}}$ is a Controlled $U$ gate that takes as input the $j$-th qubit and acts on $i$-th qubit in $0$-th index system. As I have just mentioned, the operators should be read from right to left.

If this is your first time to deal with a quantum algorithms, my advice is that you should practice calculating in both matrix and quantum fashions. That may help you really understand the process and be ready for more complicated algorithms to come.

In the next part, I’ll mainly focus on implementing the protocol using Microsoft Q# programming language.