Bernstein-Vazirani algorithm (Part 1): A derivation of the Deutsch-Jozsa algorithm

Here we stop by Berstein-Vazirani problem that inherents the structure of its predecessor, Deutsch-Jozsa problem, before we can get started with problems and solutions of practical meaning later. Because this problem is similar to the one stated in the last series, we’ll get straight to it.

Berstein-Vazirani problem

The access for a black-box function $f: \{0,1\}^n \mapsto \{0,1\}$. It’s guaranteed that $f(\mathbf{x}) = \mathbf{s}\cdot\mathbf{x}$ (mod $2$) for some secret string $\mathbf{s} \in \{0,1\}^n$.
Quest: Find $\mathbf{s}$.

Classical approach

You can get every bit of $\mathbf{x}$ one-by-one by querying $f$ with binary strings that only have one $1$, each in a different position. For example, if $\mathbf{s} = s_1s_2…s_n$, $$f(10…0) = s_1 \\ f(01…0) = s_2 \\ \vdots \\ f(00…1) = s_n$$ Queries each provides one bit of information about $\mathbf{s}$, so we need to make $n$ queries in order to retrieve $\mathbf{s}$. No classical algorithm can do anything better than this. But Bernstein, Vazirani et al. proposed a quantum algorithm, later named after them, when trying to find out a class of problems that can only be solved efficiently in the quantum world. Their original idea was revised several times and proved that $\mathbf{s}$ can be determined within one query to the oracle function $f$.

Quantum approach

In general, the solution to this problem is pretty much the same as that the solution to the Deutsch-Jozsa problem. The only two differences emerge in constructing the oracle (only during implementation) and analyzing the measurement result. The circuit for the solution is therefore unchanged.

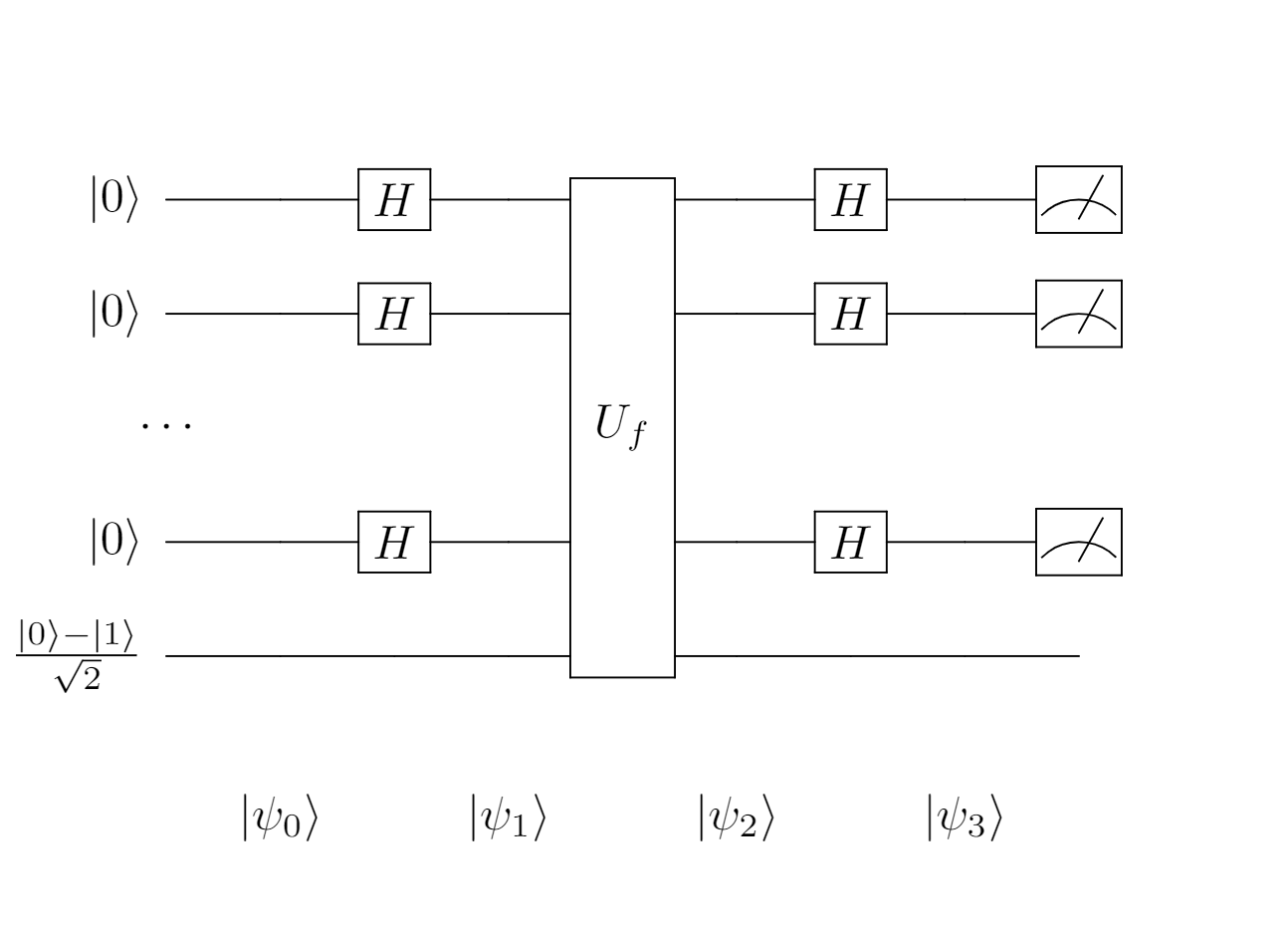$$|\psi_0\rangle = |0\rangle^{\otimes n} \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}}\right)$$ $$|\psi_1\rangle = \frac{1}{\sqrt{2^n}}\sum_{\mathbf{x} \in \{0,1\}^n} |\mathbf{x}\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}}\right)$$ $$\begin{matrix} |\psi_2\rangle & = & \displaystyle{\frac{1}{\sqrt{2^n}} \sum_{\mathbf{x} \in \{0,1\}^n} (-1)^{f(\mathbf{x})} |\mathbf{x}\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)} \\ & = & \displaystyle{\frac{1}{\sqrt{2^n}} \sum_{\mathbf{x} \in \{0,1\}^n} (-1)^{\mathbf{s}\cdot\mathbf{x}} |\mathbf{x}\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}\end{matrix}$$

In the last series, we saw that the compound Hadamard transform acting on the first register can be expressed as $H^{\otimes n} |\mathbf{x}\rangle = \frac{1}{\sqrt{2^n}} \sum_{\mathbf{z} \in \{0,1\}^n} (-1)^{\mathbf{x} \cdot \mathbf{z}} |\mathbf{z}\rangle$. Combine this expression with the last one we get

$$|\psi_3\rangle = \frac{1}{\sqrt{2^n}} \sum_{\mathbf{z} \in \{0,1\}^n} (-1)^{\mathbf{s}\cdot\mathbf{x} \oplus \mathbf{x}\cdot\mathbf{z}} |\mathbf{z}\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right) $$

Now let’s take a closer look at the coefficient of the first register. The amplitude, neglecting the global factor, is $$\begin{matrix} & \displaystyle{\sum_{\mathbf{z} \in \{0,1\}^n} (-1)^{\mathbf{s}\cdot\mathbf{x} \oplus \mathbf{x}\cdot\mathbf{z}}} \\ = & \displaystyle{\sum_{\mathbf{z} \in \{0,1\}^n} (-1)^{(\mathbf{s}\oplus\mathbf{z})\cdot \mathbf{x}}} \\ = & \displaystyle{\prod_{i=1}^n \sum_{z_i \in \{0,1\}} (-1)^{(s_i \oplus z_i)\cdot x_i}} \end{matrix}$$ At least one term of the product vanishes, thus the product becomes $0$, unless every bit $s_i$ of $\mathbf{s}$ is equal to the corresponding bit $z_i$ of $\mathbf{z}$, i.e. $\mathbf{s} = \mathbf{z}$. So, by measuring the state $|\mathbf{z}\rangle$, we actually obtain $\mathbf{s}$.

Looking back the whole process, we can reduce all transformations across the circuit to $\mathbf{H}^{\otimes (n+1)}\mathbf{U}_f\mathbf{H}^{\otimes(n+1)} |0\rangle^{\otimes n} |1\rangle = |\mathbf{s}\rangle |1\rangle$. We’re going to implement this algorithm in the next part. Two ways of constructing the oracle will be discussed.