Deutsch Algorithm (Part 1): Kicking the phase back

I have said something like quantum computing can overpower classical computing several times before. In this series, I’m going to showing you a problem with a quantum algorithm that is exponentially faster in terms of complexity than any classical solution. In this text, we’re going to explore an essential technique and apply it to solve the simplest version of Deutsch problem.

Phase kick-back

One concept you may encouter numerous times in a Linear Algebra class is eigenvalues and eigenvectors. In the setting of quantum information, we say $|\psi\rangle$ is an eigenvector of operator $U$ with eigenvalue $\lambda$ if $$U|\psi\rangle = \lambda|\psi\rangle$$

The concept is very convenient because it keeps $|\psi\rangle$ unchanged or, more accurately, results in a multiple of $|\psi\rangle$. Here we have a special instance, which is the state $\frac{|0\rangle-|1\rangle}{\sqrt{2}}$. It is an eigenvector of the $I$ (Identity) gate (undoubtedly true for all states) and the $X$ (NOT) gate simultaneously. Verifying these properties, you’ll see that $$I\left(\frac{|0\rangle-|1\rangle}{\sqrt{2}}\right) = \frac{|0\rangle-|1\rangle}{\sqrt{2}}$$ $$X\left(\frac{|0\rangle-|1\rangle}{\sqrt{2}}\right) = (-1)\frac{|0\rangle-|1\rangle}{\sqrt{2}}$$

Now we try to evaluate the effects in a 2-qubit gate $U_f$ that maps $U_f: |x\rangle|y\rangle \mapsto |x\rangle|y\oplus f(x)\rangle$ with $f$ being an arbitrary function from $\{0,1\}$ to $\{0,1\}$. Although you can never what is inside the function $f$, the whole mapping $U_f$ is reversible because the control qubit $|x\rangle$ is kept intact. We can fix the target register (another name for target qubit) to the state $\frac{|0\rangle - |1\rangle}{\sqrt{2}}$ and analyse the impact $U_f$ creates on the control register. $$\begin{matrix} \displaystyle{U_f: |x\rangle \left(\frac{|0\rangle - |1\rangle}{\sqrt{2}}\right)} & \displaystyle{\mapsto} & \displaystyle{\frac{U_f|x\rangle|0\rangle -U_f|x\rangle|1\rangle}{\sqrt{2}}}\\ & = & \displaystyle{\frac{|x\rangle|0\oplus f(x)\rangle - |x\rangle|1\oplus f(x)\rangle}{\sqrt{2}}}\\ & = & \displaystyle{|x\rangle \left( \frac{|0\oplus f(x)\rangle - |1\oplus f(x)\rangle}{\sqrt{2}} \right)}\end{matrix}$$

We know that $\oplus f(x)$ acts as an Identity operator if $f(x) = 0$ and as a NOT operator if $f(x) = 1$. This is the case I explained just before this example. So, let’s consider what occurs to the target qubit when $f(x) = 0$ and $f(x) = 1$: $$\begin{matrix} f(x) = 0 : & \displaystyle{\frac{|0\oplus f(x)\rangle - |1\oplus f(x)\rangle}{\sqrt{2}}} &= & \displaystyle{\frac{|0\rangle - |1\rangle}{\sqrt{2}}}\\ f(x) = 1 : & \displaystyle{\frac{|0\oplus f(x)\rangle - |1\oplus f(x)\rangle}{\sqrt{2}}} & = & \displaystyle{-\left(\frac{|0\rangle - |1\rangle}{\sqrt{2}}\right)}\end{matrix}$$

In these two possibilities, the posterior target states only differ by a global factor of $-1$, which depends on the value of $f(x)$. In that way, we can generalize the transformation into: $$\displaystyle{ U_f: |x\rangle \left(\frac{|0\rangle - |1\rangle}{\sqrt{2}}\right) \mapsto |x\rangle \left( \frac{|0\oplus f(x)\rangle - |1\oplus f(x)\rangle}{\sqrt{2}} \right) = (-1)^{f(x)} |x\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}$$

In most of the cases, the control qubit will be in a superposition of $|0\rangle$ and $|1\rangle$:

$$\displaystyle{ U_f: (\alpha|0\rangle + \beta|1\rangle) \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right) \mapsto \left( (-1)^{f(0)} \alpha|0\rangle + (-1)^{f(1)} \beta|1\rangle \right) \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}$$

This phase kick-back technique is definitely useful for solving some quantum problems, especially the next one.

Deutsch Problem

Trong’s crush has a apparatus that takes a binary input to compute a binary value. Mathematically, it’s a black-box function $f: \{0,1\} \rightarrow \{0,1\}$ (which means you can get the value of $f$ with different inputs but have no idea about how $f$ computes inside).
Task: Trong wants to know whether $f$ is constant or balanced by making least queries to $f$.

What is a constant function? Balanced function. A function with binary outputs is constant if it always returns one value regardless of the input. A balanced function is one that outputs $0$ in a half of circumstances and outputs $1$ in the other half. $f: \{0,1\} \rightarrow 0$ and $f: \{0,1\} \rightarrow 1$ are examples of constant functions while $f(x) = \left\{\begin{matrix} 0 \text{, if } x = 0 \\ 1 \text{, if } x = 1 \end{matrix}\right. \text{ }$ and $\text{ }f(x) = \left\{\begin{matrix} 0 \text{, if } x = 1 \\ 1 \text{, if } x = 0 \end{matrix}\right.$ are balanced. Although we have no way to decode a black-box function, it’s possible to extract some partial, relational information of the function leveraging quantum information properties. In the Deutsch problem, $f$ is constant if $f(0) \oplus f(1) = 0$ and balanced if $f(0) \oplus f(1) = 0$ that makes the problem equivalent to evaluating $f(0) \oplus f(1)$ with least queries.

Let’s start from the classical approach. How many queries are needed at least to determine $f(0) \oplus f(1)$. The answer is obviously $2$. You have to know both the values of $f(0)$ and $f(1)$. Without one of those two values, you can never conclude anything if the function is constant or balanced. On the other hand, a quantum algorithm known as Deutsch algorithm is able to achieve this within a single query.

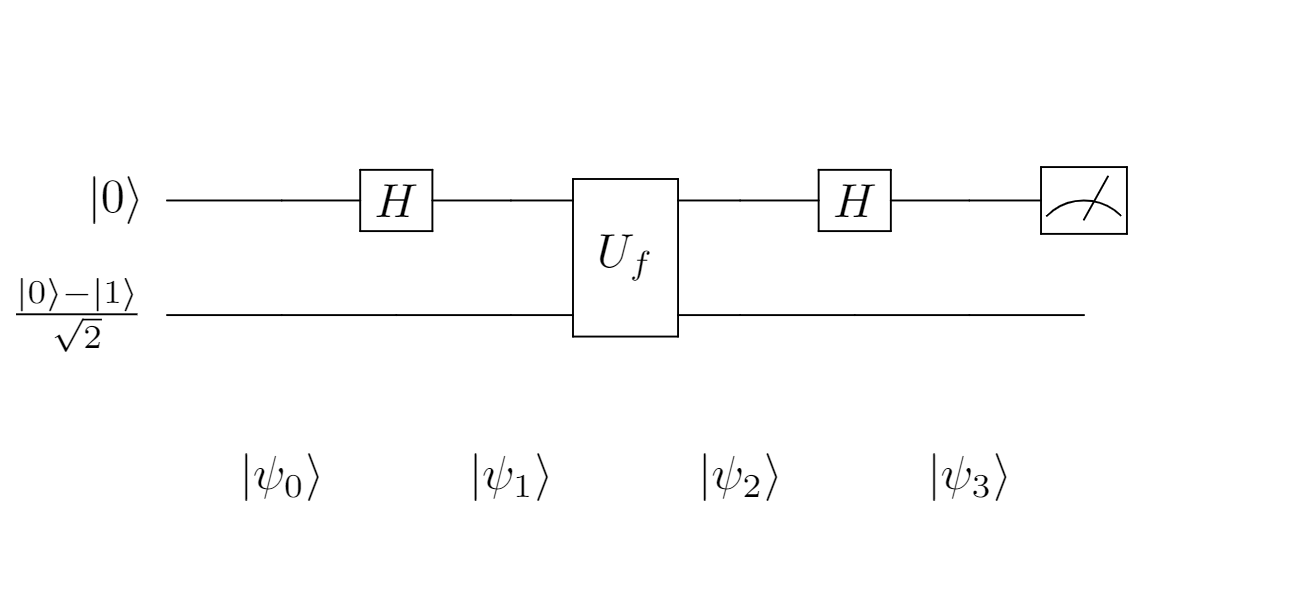
The figure above is the quantum circuit for the Deutsch algorithm. We begin with two registers, one in $|0\rangle$ and the other in $|-\rangle$. The $|-\rangle$ qubit is used because we want to exploit it in phase kick-back. This state can be craeted by applying a single Hadamard gate to $|1\rangle$, which I don’t show to emphasize the algorithm’s symmetry. If you’re curious about using $|-\rangle|0\rangle$ as our starter pack, you can reproduce the result by following the same procedure as follows:

First, as I’ve mentioned, the input state is: $$|\psi_0\rangle = |0\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)$$

Second, let a Hadamard gate act on the first qubit. The purpose of this action is to create a superposition that grants us the ability to quantumly compute on multiple combinations of states simultaneously after this stage. $$\begin{matrix} |\psi_1\rangle & = & \displaystyle{\left( \frac{|0\rangle + |1\rangle}{\sqrt{2}} \right) \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}\\ & = & \displaystyle{\frac{1}{\sqrt{2}}|0\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right) + \frac{1}{\sqrt{2}}|1\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}\end{matrix}$$

Recalling the last representation of $U_f$ shown in the phase kick-back section, after applying the $U_f$ gate and doing some basic math we have: $$\begin{matrix} |\psi_2\rangle & = & \displaystyle{\frac{(-1)^{f(0)}}{\sqrt{2}}|0\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right) + \frac{(-1)^{f(1)}}{\sqrt{2}}|1\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}\\ & = & \displaystyle{\left( \frac{(-1)^{f(0)}|0\rangle+(-1)^{f(1)}|1\rangle}{\sqrt{2}} \right) \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}\\ & = & \displaystyle{(-1)^{f(0)} \left( \frac{|0\rangle+(-1)^{f(0)\oplus f(1)}|1\rangle}{\sqrt{2}} \right) \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)}\end{matrix}$$

In the last line we have conveniently factored out $(-1)^{f(0)}$ to the global phase, leaving $(-1)^{f(0)\oplus f(1)}$ as a relative phase. It’s possible to ignore the global phase because it’s unobservable and thus has no experimental meaning. With that in mind, we can see that if $(-1)^{f(0)\oplus f(1)} = 0$ when $f$ is constant, the first qubit is left in the stage $\frac{|0\rangle + |1\rangle}{\sqrt{2}}$. In contrast, if $(-1)^{f(0)\oplus f(1)} = 1$ when $f$ is balanced, the first qubit becomes $\frac{|0\rangle - |1\rangle}{\sqrt{2}}$. The two possibilities resulting from two situations of $f$ are easily distinguished with a measurement in Hadamard basis.

If $f$ is constant, or $(-1)^{f(0)\oplus f(1)} = 0$, $$|\psi_3\rangle = (-1)^{f(0)}|0\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)$$ If $f$ is balanced, or $(-1)^{f(0)\oplus f(1)} = 1$, $$|\psi_3\rangle = (-1)^{f(0)}|1\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)$$

At this point you should see that the type of $f$ is associated with $f(0) \oplus f(1)$ and this sum associated with the technique of kicking back phase factors (corresponding to control register’s state). The concept of using quantum interference to find out the relative amplitude is applied in this text and the next one. The real exponential speedup is coming soon…