Quantum Measurement: Not just 0 and 1

Quantum entanglement is, by definition, a phenomenon that the combined state of a set of qubits cannot be described as a product of the states of each qubit of that set, which also means the entangled state contains hidden information that one cannot reveal through examining separate qubits. In this text, I’m going to introduce and discuss several aspects of this spectacular phenomenon.

Measurement in different bases

In previous posts, I’ve mentioned that a qubit can be in a superposition of its basis states $\left|0\right\rangle$ and $\left|1\right\rangle$ with corresponding complex amplitudes $a_0$ and $a_1$. Let’s take a look at a specific instance of equal amplitude coefficients $$\left|\psi\right\rangle = \frac{1}{\sqrt{2}}\left|0\right\rangle + \frac{1}{\sqrt{2}}\left|1\right\rangle$$ Called an equal superposition, the state turns into either $\left|0\right\rangle$ or $\left|1\right\rangle$ with equal probability of $\displaystyle{\left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2}}$ in a measurement. In fact, the possible results are just the outcome of a measurement in Pauli $Z$ basis that includes $\left|0\right\rangle$ and $\left|1\right\rangle$ basis states. For simplicity, qubit states will be geometrically illustrated in two dimensions, i.e. probability amplitudes are real numbers.

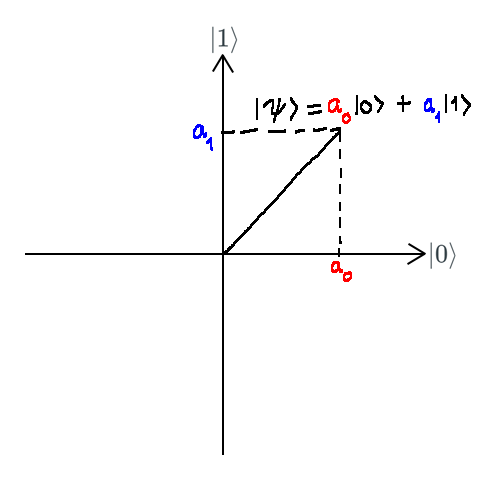
It’s clear that one get $a_0$ and $a_1$ by projecting $\left|\psi\right\rangle$ onto two standard basis vectors. Applying the same process in any other basis consisting of two arbitrary orthonormal basis vectors results in a different pair of amplitudes.

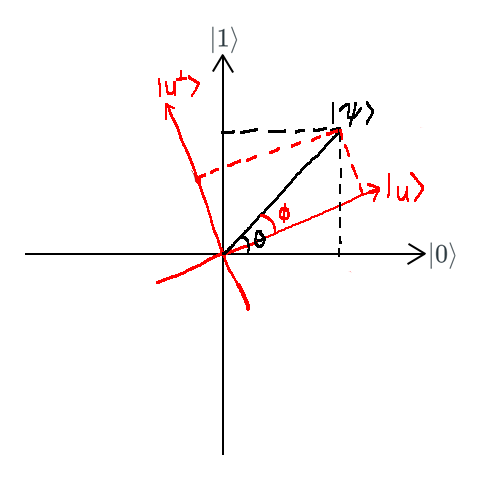
Let $\left|u\right\rangle$ and $\left|u^{\perp}\right\rangle$ be the two orthogonal basis states of a computational basis. A superposition $\left|\Psi\right\rangle$ can be measured in two distinct bases as the following: $$\left|\psi\right\rangle = \cos{(\theta)}\left|0\right\rangle + \sin{(\theta)}\left|1\right\rangle$$ $$\left|\psi\right\rangle = \cos{(\phi)}\left|u\right\rangle + \sin{(\phi)}\left|u^{\perp}\right\rangle$$ Suppose that the qubit corrupts into $\left|0\right\rangle$ in a measurement in the standard basis, if we take another measurement in the basis $\left|u\right\rangle, \left|u^{\perp}\right\rangle$ on the corrupted qubit, its state will turn into either $\left|u\right\rangle$ or $\left|u^{\perp}\right\rangle$ with probability $\cos^2{(\theta - \phi)}$ and $\sin^2{(\theta - \phi)}$ respectively. $$\left|\psi\right\rangle = \left|0\right\rangle= \cos{(\theta - \phi)}\left|u\right\rangle - \sin{(\theta - \phi)}\left|u^{\perp}\right\rangle$$ The most used $\left|u\right\rangle$ and $\left|u^{\perp}\right\rangle$ are equal superposition states $\left|+\right\rangle$ and $\left|-\right\rangle$ that together form the sign basis with $$\left|+\right\rangle = \frac{1}{\sqrt{2}}\left|0\right\rangle + \frac{1}{\sqrt{2}}\left|1\right\rangle$$ $$\left|-\right\rangle = \frac{1}{\sqrt{2}}\left|0\right\rangle - \frac{1}{\sqrt{2}}\left|1\right\rangle$$

Measurement of multiple qubits

In the case of two qubits, the general state is constrained by the normalization condition. $$\left|\Psi\right\rangle = \alpha_{00}\left|00\right\rangle + \alpha_{01}\left|01\right\rangle + \alpha_{10}\left|10\right\rangle + \alpha_{11}\left|11\right\rangle,$$ $$\left|\alpha_{00}\right|^2 + \left|\alpha_{01}\right|^2 + \left|\alpha_{10}\right|^2 + \left|\alpha_{11}\right|^2 = 1$$ If one measure the first qubit, it will return $\left|0\right\rangle$ with possibility $(a_{00}^2 + a_{01}^2)$ or $\left|1\right\rangle$ with possibility $(a_{10}^2 + a_{11}^2)$. Whatever the result is, the first qubit will permanently turn into that state, having an effect on the whole state also due to the normalization constraint. Assume the state of the first qubit after measurement is $\left|0\right\rangle$, then the combined state is transformed into $$\left|\Psi\right\rangle = \frac{\alpha_{00}}{\sqrt{\alpha_{00}^2+\alpha_{01}^2}}\left|00\right\rangle + \frac{\alpha_{01}}{\sqrt{\alpha_{00}^2+\alpha_{01}^2}}\left|01\right\rangle$$ The current state indicates that one can only get $\left|00\right\rangle$ or $\left|01\right\rangle$ depending on a measurement of the second qubit. That a measurement can narrow down the number of possibilities of the posterior state with regard to the measurement outcome can shed some light on a strange quantum behavior called Quantum Entanglement. I’ll introduce the phenomenon and its significance through some trivial game next time.