Deutsch Algorithm (Part 2): Deutsch-Jozsa problem - The first exponential speedup

Here we’re gonna see the most impressive quantum algorithm in terms of query complexity. The algorithm is an generalization of the original Deutsch algorithm we discussed in the last post. But I want to say that this algorithm may not be as extraordinary as you may think of it. It was created to solve a kind of problem that has zero practical meaning for the purpose of demonstrating how strong quantum computing can reach compared to classical computing. Telling that truth doesn’t mean to disappoint you. I just want you to be aware that quantum computing is never a universal key to our computation problems. If it is the powerful key to break all classical limits, the field should be much more developed at this time. Although not having a significant value, the Deutsch-Jozsa problem and algorithm still teach us some interesting concepts such as phase kickback, oracle design, and circuit construction that are definitely useful for more complicated issues upcoming.

Deutsch-Jozsa Problem

The problem generalizes the original version’s black box $f$ into a function that takes a bit string of length $n$ as input and returns a binary value, $f: \{0,1\}^n \rightarrow \{0,1\}$ where $n$ is an arbitrary positive integer. $f$ is guaranteed to be constant or balanced. Your quest is the unchanged: determine whether $f$ is constant or balanced with least queries to $f$.

If we want to solve this problem classically, we’ll need to make $2^{n-1}+1$ queries in the worst case. That worst case occurs when $f$ is balanced, and you’re lucky (or unlucky) enough to get a single output by the time you query for half of possible inputs, i.e. $2^{n-1}$ different input bit string. You need to query one more time to answer the problem with perfect certainty. In this case $2^{n-1} + 1$ increases exponentially as the bit string rises in size.

If we accept a failure with probability of $\epsilon$, then randomly choose $k$ different $x_k$ to query. This probabilistic algorithm requires query complexity $k = \mathcal{O}\left( \log{\left( \frac{1}{\epsilon}\right)} \right)$.

Here comes the the revised Deutsch algorithm that do the same task in exactly one query. Same as in the first part, we start with two quantum registers. First, a control register contains $n$ qubits initiated in the state of $|0\rangle^{\otimes n}$ that represents $n$ qubits all in the $|0\rangle$ state. Second, a target register started in the state $\frac{|0\rangle - |1\rangle}{\sqrt{2}}$ to exploit the phase kickback effect.

The quantum circuit for the algorithm is generalized from its simplified version:

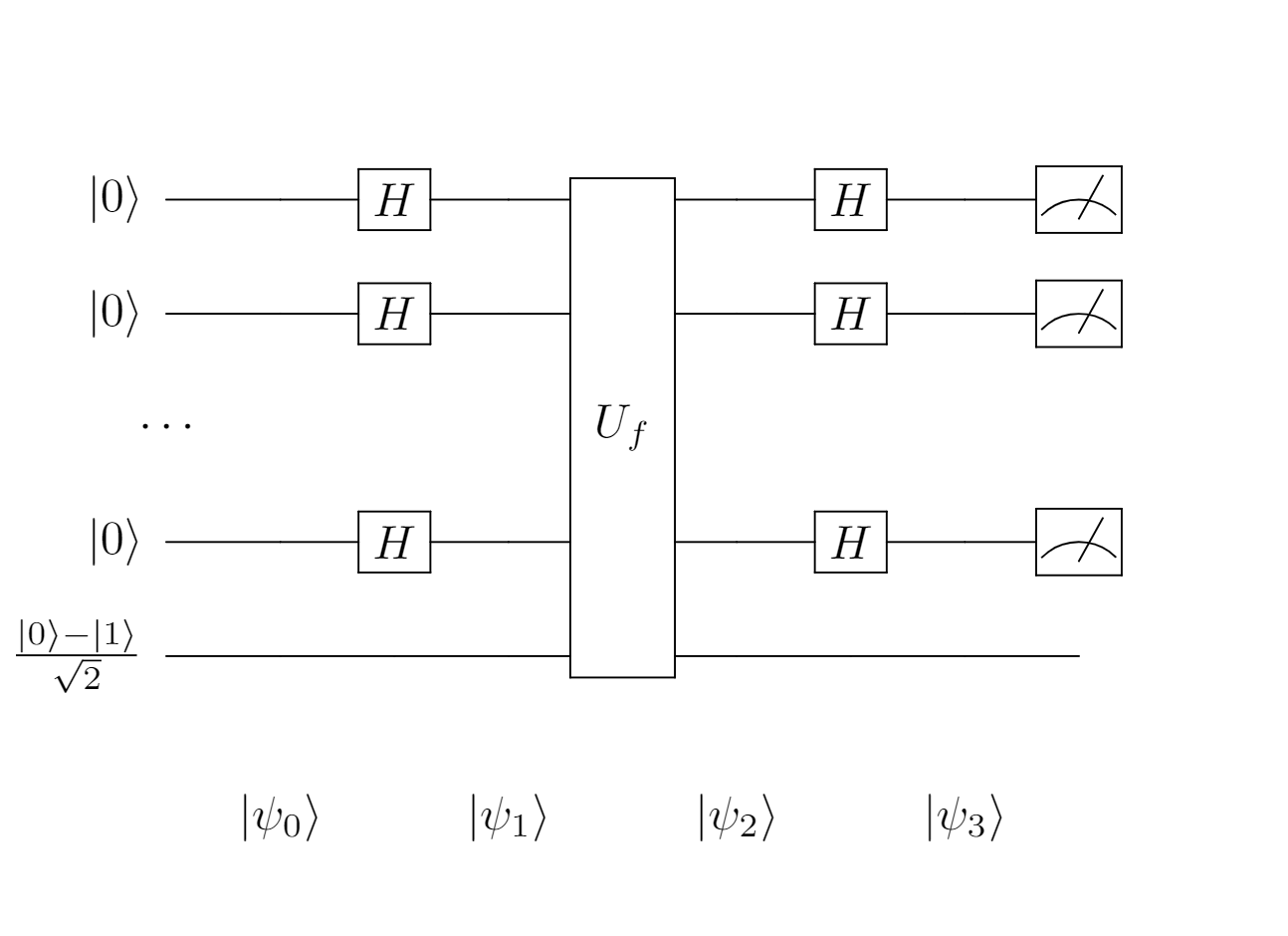$$|\psi_0\rangle = |0\rangle^{\otimes n}\frac{|0\rangle - |1\rangle}{\sqrt{2}}$$

The action of $n$ Hadamard gates on the first register is to create an equal superposition of all possible composite states in the complex vector space $\mathbb{C}^n$.

$$|\psi_1\rangle = \frac{1}{\sqrt{2^n}} \sum_{\mathbf{x} \in \{0,1\}^n} |\mathbf{x}\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)$$

I write $x$ in boldface to emphasize $\mathbf{x}$ is a string, not a single number. $|\psi_1\rangle$ can also be represented using decimal indexes rather than binary strings for quantum states: $$|\psi_1\rangle = \frac{1}{\sqrt{2^n}} \sum_{x = 0}^{2^n-1} |x\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)$$

We construct an operator $U_f: |\mathbf{x}\rangle |y\rangle \mapsto |\mathbf{x}\rangle |y \oplus f(\mathbf{x})\rangle$. We’ll see that the function $f$ having effect on the second register leaves the first register with a factor of $(-1)^{f(\mathbf{x})}$. $$\begin{matrix} |\psi_2\rangle & = & \displaystyle{\frac{1}{\sqrt{2^n}} \sum_{\mathbf{x} \in \{0,1\}^n}^{2^n-1} |x\rangle \left( \frac{|0 \oplus f(\mathbf{x}) \rangle - |1 \oplus f(\mathbf{x}) \rangle}{\sqrt{2}} \right)} \\ & = & \displaystyle{\frac{1}{\sqrt{2^n}} \sum_{\mathbf{x} \in \{0,1\}^n} (-1)^{f(\mathbf{x})} |\mathbf{x}\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)} \end{matrix}$$

Now what we should do is applying Hadamard transformation to all qubits in the first register. To see why we need to do that, we should take a look at an instance of $2$ qubits in the first register after oracle $U_f$. When $n=2$, the first register of $|\psi_2\rangle$ becomes

$$\frac{1}{\sqrt{2^2}} \sum_{\mathbf{x} \in \{0,1\}^2} (-1)^{f(\mathbf{x})} |\mathbf{x}\rangle = \frac{(-1)^{f(00)}|00\rangle + (-1)^{f(01)}|01\rangle + (-1)^{f(10)}|10\rangle + (-1)^{f(11)}|11\rangle}{2}$$

If $f(\mathbf{x})$ is constant, then $(-1)^{f(\mathbf{x})}$ must be equal to $1$ or $-1$ for all values of $\mathbf{x}$. In that case, the state shown above is an equally weighted superposition with a global phase factor of $1$ if $f(x) = 0$ and an equally weighted superposition with a global phase of $-1$ if $f(x) = 1$. Because global factors have no practical meaning, both possibilities are the same and can be reverted into $|00\rangle$ using Hadamard transformations. On the other hand, if $f$ is balanced, we’re assured to get anything except for $|00\rangle$. Here, we’ll see a few cases, but feel free to check whether this property holds for other $n$ values and partitions. $$H^{\otimes 2} \left( \frac{|00\rangle - |01\rangle - |10\rangle + |11\rangle}{2} \right) = |11\rangle$$ $$H^{\otimes 2} \left( \frac{|00\rangle - |01\rangle + |10\rangle - |11\rangle}{2} \right) = |01\rangle$$

Now we have to establish a format math concept that illustrate the transformation. The action of a Hadamard gate on a single qubit in a $1$-qubit basis state $|x\rangle$ can be written as $$\begin{matrix} H|x\rangle & = & \displaystyle{\frac{1}{\sqrt{2}} \left( |0\rangle + (-1)^x|1\rangle \right)} \\ & = & \displaystyle{\frac{1}{\sqrt{2}} \sum_{z \in \{0,1\}} (-1)^{xz}|z\rangle} \end{matrix}$$

Noted that this can extend linearly for a superposition $|x\rangle$. We generalize the equality above to an $n$-qubit basis state $|\mathbf{x}\rangle = |x_1\rangle|x_2\rangle\cdots|x_n\rangle$: $$\begin{matrix} H^{\otimes n} |\mathbf{x}\rangle & = & H^{\otimes n}|x_1\rangle|x_2\rangle\cdots|x_n\rangle \\ & = & H|x_1\rangle H|x_2\rangle \cdots H|x_n\rangle \\ & = & \displaystyle{\frac{1}{\sqrt{2}} \sum_{z \in \{0,1\}} (-1)^{x_1z}|z\rangle \otimes \frac{1}{\sqrt{2}} \sum_{z \in \{0,1\}} (-1)^{x_2z}|z\rangle \otimes \cdots \otimes \frac{1}{\sqrt{2}} \sum_{z \in \{0,1\}} (-1)^{x_nz}|z\rangle} \\ & = & \displaystyle{\frac{1}{\sqrt{2^n}} \sum_{z_1,z_2,…,z_n \in \{0,1\}} (-1)^{x_1z_1 + x_2z_2 + … + x_nz_n} |z_1\rangle |z_2\rangle … |z_n\rangle} \\ & = & \displaystyle{\frac{1}{\sqrt{2^n}} \sum_{\mathbf{z} \in \{0,1\}^n} (-1)^{\mathbf{x} \cdot \mathbf{z}} |\mathbf{z}\rangle }\end{matrix}$$ where the bitwise inner product $\mathbf{x} \cdot \mathbf{z} = x_1z_1 + x_2z_2 + … + x_nz_n$ module $2$. The final state prior to measurements is $$\begin{matrix} |\psi_3\rangle & = & \displaystyle{ \left( \frac{1}{\sqrt{2^n}} \sum_{\mathbf{x} \in \{0,1\}^n} (-1)^{f(\mathbf{x})} \frac{1}{\sqrt{2^n}} \sum_{\mathbf{z} \in \{0,1\}^n} (-1)^{\mathbf{x} \cdot \mathbf{z}} |\mathbf{z}\rangle \right) \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)} \\ & = & \displaystyle{\frac{1}{2^n} \sum_{\mathbf{z} \in \{ 0.1 \}^n} \left( \sum_{\mathbf{x} \in \{0,1\}^n} (-1)^{f(\mathbf{x}) + \mathbf{x}\cdot\mathbf{z}} \right) |\mathbf{z}\rangle \left( \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right)} \end{matrix}$$

For the reason I’ve mentioned above, we’ll see the amplitude of $|\mathbf{z}\rangle = |0\rangle^{\otimes n}$. This amplitude is $$\frac{1}{2^n} \sum_{\mathbf{x} \in \{ 0,1 \}^n} (-1)^{f(\mathbf{x})}$$ We evaluate the amplitude in the two cases, $f$ constant and $f$ balanced. If $f$ is constant, all terms in $\sum_{\mathbf{x} \in \{ 0,1 \}^n} (-1)^{f(\mathbf{x})}$ add up together, resulting in the amplitude of $|0\rangle^{\otimes n}$ being either $+1$ and $-1$. So when $f$ is constant, the measurements on the first qubits would return a binary strings $00…0$ with probability 100%. On the other hand, if $f$ is balanced, because the number of positive terms and negative terms in $\sum_{\mathbf{x} \in \{ 0,1 \}^n} (-1)^{f(\mathbf{x})}$ are the same, they cancel out each other, and the eventual coefficient of $|0\rangle^{\otimes n}$ is $0$. So when $f$ is balanced, the measurement result can by anything EXCEPT $00…0$.

After the final measurements, we can conclude whether $f$ is constant or balanced. If the result is $00…0$, $f$ is constant. Not $00…0$, $f$ is balanced.

In the next part of this series, we’ll examine how Deutsch-Jozsa algorithm is implemented. Especially, it’ll focus on how to construct $U_f$ from $1$-qubit and $2$-qubit gates, which is an important facet of quantum algorihm but never thoroughly discussed. I’ll also introduce a minor improvement for the algorithm that only uses one register of $n$ qubits.