/ #project #Teleportation 

Quantum Teleportation (Part 3): Implementation

Let’s implement and verify the teleporation protocol following the procedure we discussed throughout previous parts.

First we need to create an arbitrary quantum state. Trong has been curious about the combined effect of rotation gates about the x, y, and z axes. So, he decides to apply three distinct rotation gates, each as a rotation of 60 degrees around one coordinate axis acting on a qubit currently in the Hadamard state $|-\rangle$. All of these steps are wrapped up in the ‘initializeFirstQubit’ operation.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
 operation initializeFirstQubit(q: Qubit) : Unit {
	// My desired state is the state created by rotating state |-⟩ 60 degrees about x, y, and z axes respectively.
	//Start from |0>
	X(q);
	H(q);
	Rx(PI()/3.0, q);
	Ry(PI()/3.0, q);
	Rz(PI()/3.0, q);
	//The final state will be be 0.9659|0⟩ - 0.2588|1⟩, so the probabilities are expected to be 0.9330 and 0.0670
 }

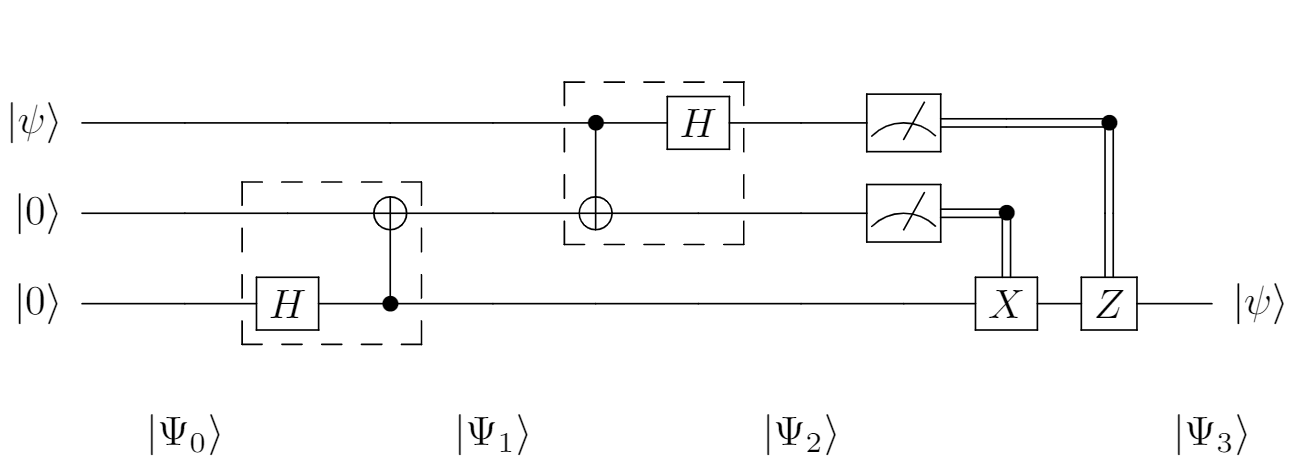
Now it's time to play teleporting. I'll also show the circuit diagram here ahead of time to make it easy for you to follow.

Example image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
   
 operation Teleportation (count: Int) : (Int, Int) {
	mutable countZero = 0;
	mutable countOne = 0;

   	using (qs = Qubit[3]) {
		for (test in 0..count) {
			// Create a special state a|0⟩ + b|1⟩ for the first qubit
			initializeFirstQubit(qs[0]);

			// Create Bell state for the two other qubits
			H(qs[2]);
			CNOT(qs[2], qs[1]);

			// Entangle the first qubit to the pair in Bell state and change the basis for the first qubit
			CNOT(qs[0],qs[1]);
			H(qs[0]);

			// Measure and Restore based on measurements
			if (M(qs[1]) == One) {
				X(qs[2]);
			}
			if (M(qs[0]) == One) {
				Z(qs[2]);
			}

			// Measure the final qubit to statistically determine which state it's in 
			if (M(qs[2]) == Zero) {
				set countZero = countZero + 1;
			}
			else {
				set countOne = countOne + 1;
			}

			ResetAll(qs);
		}			
	}

	return (countZero, countOne);
 }

The final is a program driver that runs our main operation $10000$ times and return probabilities, i.e. the squares of probability amplitudes. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
   
 class Driver {
    static void Main(string[] args) {
        using (var qsim = new QuantumSimulator()) {
            var res = Teleportation.Run(qsim, 10000).Result;
            var (prob_0, prob_1) = res;
            System.Console.WriteLine(
             $"The probabilities of getting 0 and 1 are {prob_0/10000.0} and {prob_1/10000.0}");
            Console.WriteLine("Press any key to continue...");
            Console.ReadKey();
        }
    }
 }

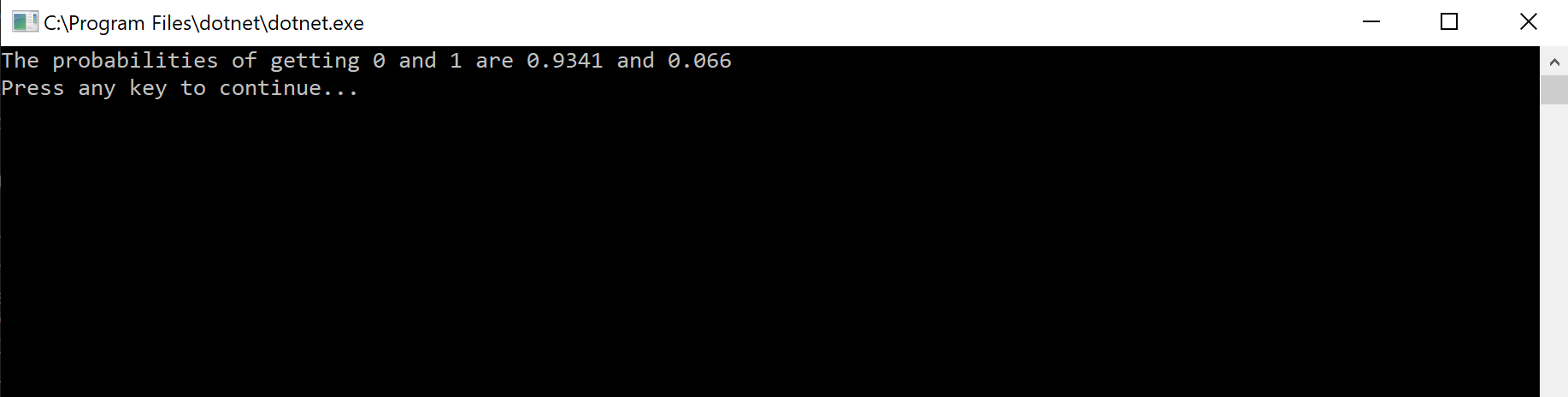
Example image

Now is your turn. In order to verify our programming result, you need to find out the state created by ‘initializeFirstQubit’. Some Python coding or calculating with pencil and paper, you can get your hand dirty by one way or the other. The matrix formulas for the rotations are as follows

$$R_x(\theta) = \begin{bmatrix} \cos{\frac{\theta}{2}} & -i\sin{\frac{\theta}{2}} \\ \cos{\frac{\theta}{2}} & \cos{\frac{\theta}{2}}\end{bmatrix}, R_y(\theta) = \begin{bmatrix} \cos{\frac{\theta}{2}} & -\sin{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} \end{bmatrix}, R_z(\theta) = \begin{bmatrix} e^{-\frac{i\theta}{2}} & 0 \\ 0 & e^{\frac{i\theta}{2}} \end{bmatrix}$$

Do it, don’t be a lazy ass like my servant.

And here’s the resulting coefficients $$R_z(\frac{\pi}{3})R_y(\frac{\pi}{3})R_x(\frac{\pi}{3})|-\rangle \approx 0.9659|0\rangle - 0.2588|1\rangle$$ It’s easy to see the displayed results get in line with our calculation. So, the code works as expected. Feel free to experiment with the here.

Author

Entangled Cat

I work hard so that my cats can live a better live